by R. Grothmann
This notebook computes reflections on a Billard table. How many possible ways exist to reach one point from another in a round Billiard table?
The following function computes the length of a path in the complex plane from z0 to z and then to z1.
>function d(z0,z1,z) := abs(z-z0)+abs(z-z1)
Now we define a circle in the complex plane.
>t=linspace(0,2*pi,300); z=exp(1i*t);
We plot all distances between two given points via the circle.
>z0=0.5+0.5i; z1=-3/5; plot2d(t,d(z0,z1,z)):
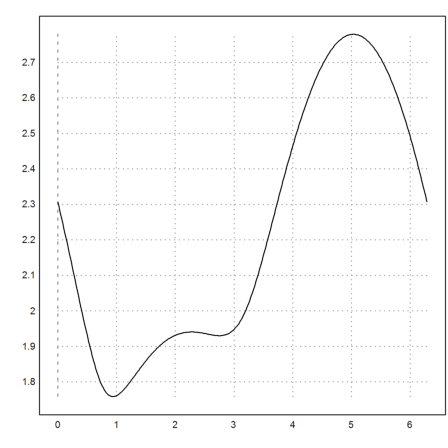
There are four local extrema, which are related to paths that obey the law of reflections.
Let us define a function, which computes the round trip over e^(it).
>function f(t,z0,z1) := d(z0,z1,exp(1i*t));
Now we use the function fextrema() to compute all local extrema.
>{mi,ma}=fextrema("f",0,2*pi,400;z0,z1); "Minima:", mi, "Maxima", ma,
Minima: [0.938077, 2.75097] Maxima [2.2748, 5.03173]
>plot2d(z); ... hold on; mark(z0); mark(complex(z1)); hold off; ... hold on; plot([z0,exp(1i*mi[1]),z1]); hold off; ... hold on; plot([z0,exp(1i*mi[2]),z1]); hold off; ... hold on; plot([z0,exp(1i*ma[1]),z1]); hold off; ... hold on; plot([z0,exp(1i*ma[2]),z1]); hold off:
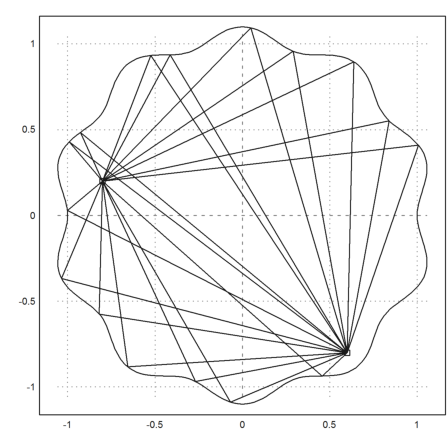
We see that there are four ways to play a Billiard ball with one reflection from z0 zo z1.
We want to define a function that does the same for a general curve. First we define our curve.
>function gamma0(t) := exp(1i*t);
Now we define a function for the round trip, calling the curve function by name.
>function f1 (t,fff,z0,z1) := d(z0,z1,fff(t));
Next, we make a function, which plots the curve, computes the minima and maxima, and plots the distances.
>function billiard (fgamma,z0,z1) ...
keepsquare(1);
t=linspace(0,2*pi,300); xplot(fgamma(t));
hold on;
mark(complex(z0)); mark(complex(z1));
{mi,ma}=fextrema("f1",0,2*pi,300;fgamma,z0,z1);
loop 1 to cols(mi);
plot([z0,fgamma(mi[#]),z1]);
end;
loop 1 to cols(ma);
plot([z0,fgamma(ma[#]),z1]);
end;
keepsquare(0);
hold off;
endfunction
>billiard("gamma0",z0,z1):
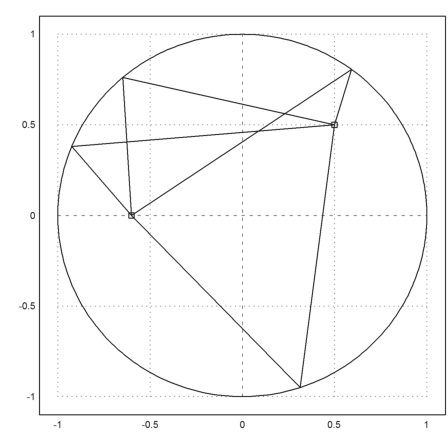
Now we take an elliptic table.
>function gamma1(t) := cos(t)+0.8i*sin(t); ...
billiard("gamma1",-0.6-0.3i,0.5+0.5i):
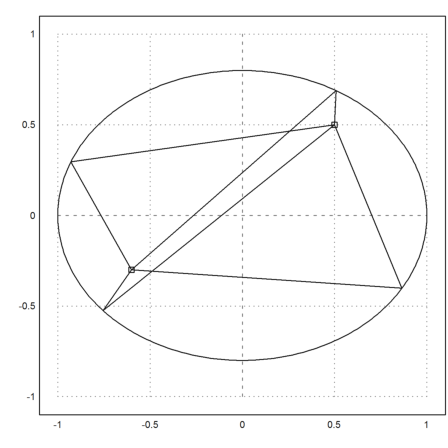
Finally, something weird.
>function gamma2(t) := (cos(t)+1i*sin(t))*(1+sin(5*t)^2/10); ...
billiard("gamma2",-0.8+0.2i,0.6-0.8i):