by R. Grothmann
This is just a fun application. A Pana cotta (could be any other pudding) is cooling down. The measurements were
at 0 min : 66°
at 30 min : 53.5°
at 60 min : 44.6°
The measurements are somewhat inaccurate, since the Pana cotta was stirred, windows were opened etc. However, what is the room temperature, and when will the Pana cotta have reached 35°?
We use the following model for our cooling.
![]()
whera a is the temperature of the room.
>function f(t,a,b,c) := a+exp(b*t-c)
Enter the measurements.
>t=[0,30,60]; T=[66,53.5,44.6]; >plot2d(t,T,points=1); plot2d(t,T,add=1):
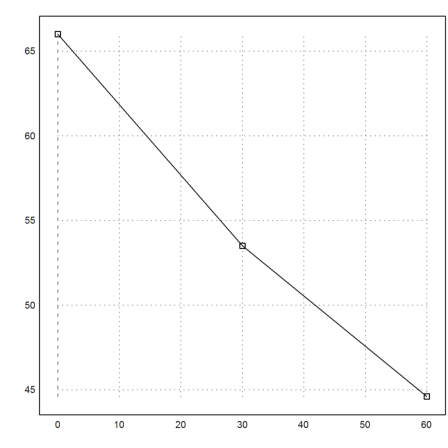
Now we want to interpolate the function. We use Nelder-Mead for this.
The following is the error.
>function delta (v) := totalmax(abs(T-f(t,v[1],v[2],v[3])))
It turns out, that we need a good starting point. So we use a guess for a, the room temperature, and fit b and c according to log(M-a) = bt-c.
>a=20; M=t'|-1; b=log(T-a)'; >w=fit(M,b); b=w[1], c=w[2]
-0.0104315825592 -3.82725856953
This does not quite interpolate.
>delta([a,b,c])
0.0927776426688
So we apply Nelder-Mead. The room temperature should be 22.5°.
>w=neldermin("delta",[a,b,c]), a=w[1]; b=w[2]; c=w[3];
[22.5972, -0.0113226, -3.77052]
Plot the result.
>plot2d("f(x,a,b,c)",0,240); plot2d(t,T,points=1,add=1):
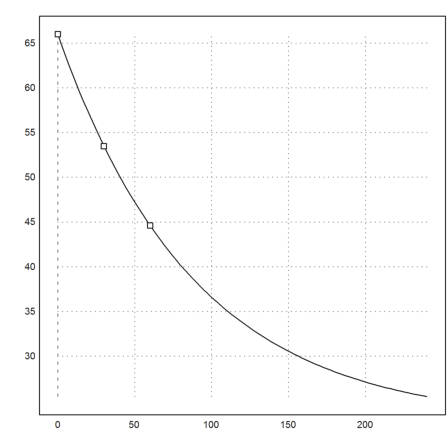
Solve for the time. After 156 min the Pana cotta should have 30°.
>solve("f(x,a,b,c)",120,y=30)
156.207181302
The true room temperature was about 24°. Let us try to fix that with another measurement.
>t=t|85; T=T|40.2;
>w=neldermin("delta",[a,b,c]), a=w[1]; b=w[2]; c=w[3];
[28.2825, -0.0138396, -3.63589]
So we get another room temperature. Probably the method of measurement should have been more scientific.
>plot2d("f(x,a,b,c)",0,240); plot2d(t,T,points=1,add=1):
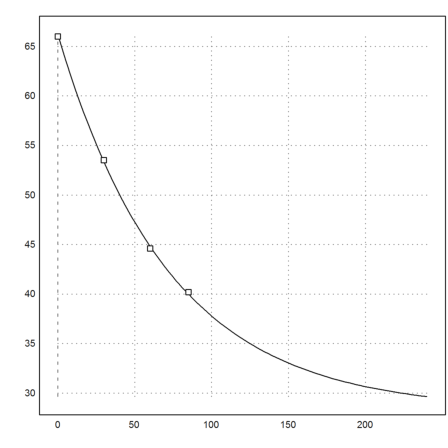
The predicted time is very sensitive to these errors, since it is close to the room temperature.
>solve("f(x,a,b,c)",120,y=30)
223.637373862
After 125 minutes, the predicted temperature is 34.6°.
>f(125,a,b,c)
35.0083063303
In reality, it was 35°. Let us add this to our data.
>t=t|125; T=T|35.0;
>w=neldermin("delta",[a,b,c]), a=w[1]; b=w[2]; c=w[3];
[28.4844, -0.0139632, -3.63019]
>plot2d("f(x,a,b,c)",0,240); plot2d(t,T,points=1,add=1):
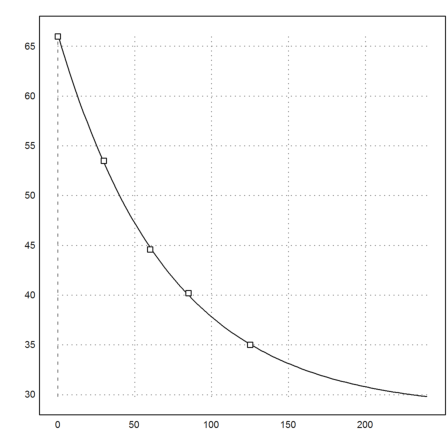
>solve("f(x,a,b,c)",120,y=30)
230.201564176