by R. Grothmann
In this notebook, you can design a rotation object with just a few mouse clicks.
First we define a function to read the mouse clicks in a loop.
>function getpoints ...
setplot(-1,1,-1,1); clg; xplot();
title("Click into the half plane x>0");
v=zeros(0,2);
repeat
m=mouse(); if cols(m)==1 then break; endif;
v=v_m;
hold on; style("mx"); mark(m[1],m[2]); hold off;
end;
return v
endfunction
Now you can try it. Click into right half plane x>0 with monotone decreasing y.
>v=getpoints()
0.590692 0.980257
0.207214 0.706317
0.123849 0.506781
0.133853 0.128
0.287244 -0.0512448
0.520666 -0.223725
0.594027 -0.389442
0.520666 -0.656618
0.490655 -0.842627
0.667388 -0.910266
0.930821 -0.930558
The following commands compute a natural spline, joining the points.
>v=v'; n=cols(v); x=1:n; ... s1=spline(x,v[1]); s2=spline(x,v[2]); ... t=linspace(1,n,600); ... y1=splineval(t,x,v[1],s1); y2=splineval(t,x,v[2],s2); ... hold on; plot(y1,y2); hold off:
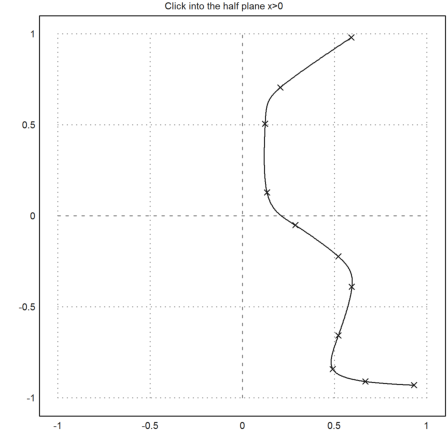
Now generate a 3D object from these points.
>phi=linspace(0,2*pi,200)'; >X=cos(phi)*y1; Y=sin(phi)*y1; Z=y2;
And plot it.
>plot3d(X,Y,Z,hue=1,frame=0,height=30°, ... zoom=4,<scale,color=rgb(0.2,0,0),amb=0):
