We start with two bodies in space. The function test3body uses an adaptive Runge method to solve the Newtonian equations for the movements of bodies under gravitation.
>load 3body;
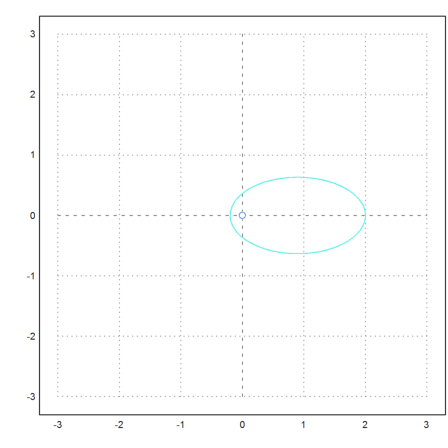
In the first example, we take two bodies with equal weight, starting with equals speed. The initial positions and speed vectors are
![]()
![]()
The time interval is one second, and this interval is subdivided into n=100 subintervals by default.
Euler animates the movement of the planets. To save time, the animation is very coarse.
>test2body([-2,0, 2,0, 0,-0.3, 0,0.3],tmax=30):
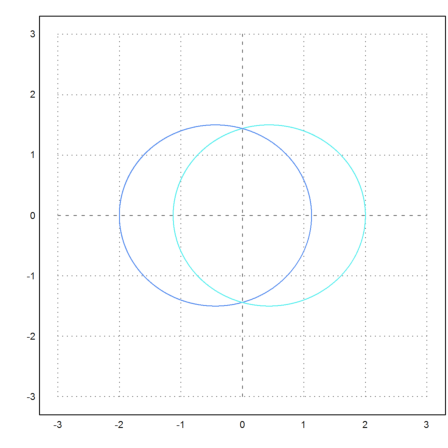
The next example has two different masses. For a smoother animation, we take a time interval of 0.1.
>test2body([0,0, 2,0, 0,-0.2, 0,2],m1=10,m2=1,tmax=5,h=0.1):
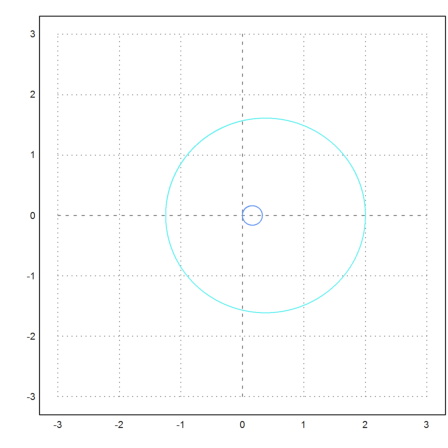
The display can be centered at the first mass. We change the initial speed of the second mass a bit.
>test2body([0,0, 2,0, 0,0, 0,1],m1=10,m2=1,tmax=5,>fixed):
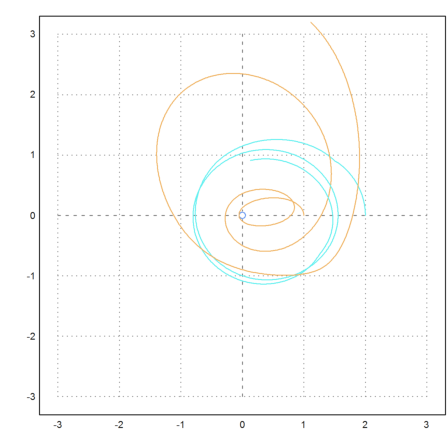
With three bodies, the movements get chaotic.
>test3body([-2,0, 2,0, 0,2, 0.1,-0.2, -0.2,0.2, 0.1,0],n=100):
One body left definition area!
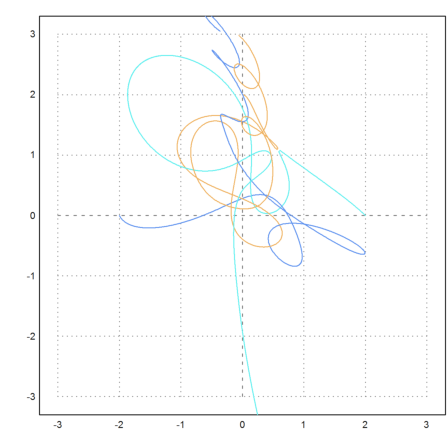
The accuracy is critical here, since the bodies get very close to each other. If you like try n=1000. Then the behaviour does not change much, so we assume that the computation is accurate.
The next example has two starts of mass 1 and 2, and a plante of mass 0.1. The planet will run around the larger star until the smaller one catches the planet for a short time.
>test3body([0,0, 2,0, 1,0, 0,0, 0,1.3, 0,1.2], ... m1=2,m2=1,m3=0.1,>fixed,tmax=50):

With slightly different initial conditions the small planet gets kicked out of the system very soon.
>test3body([0,0, 2,0, 1,0, 0,0, 0,1, 0,0.5], ... m1=2,m2=1,m3=0.1,>fixed,tmax=10):